一，晏略殊定理

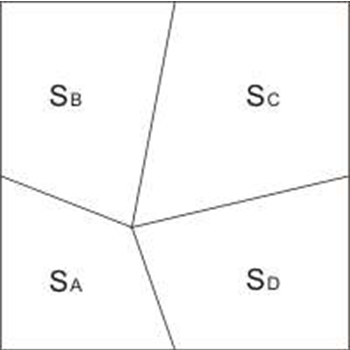
（一），定理内容：正方形内任意一点，向其各边中点的连线，构成四个不规则的四边形，其中相对的两个四边形面积之和等于另外两个相对四边形的面积之和。

 

（二），证明：

设：S1+S2 =SA

S3+S4 =SB

S5+S6 =SC

S7+S8 =SD

 

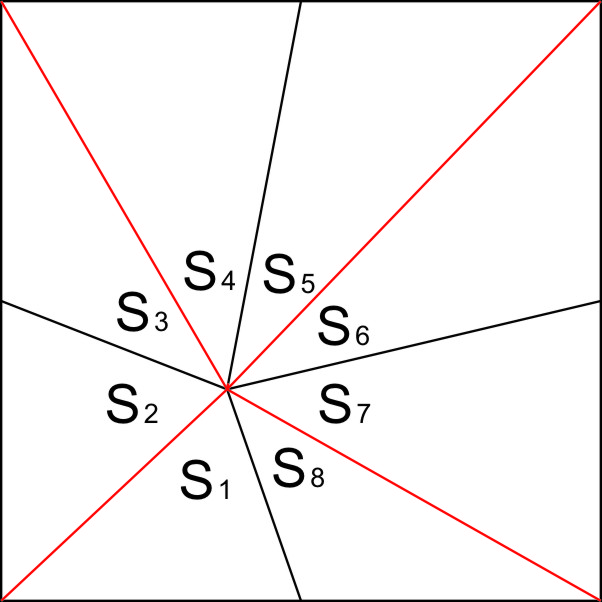
SA+SC=S1+S2+S5+S6
SB+SD=S3+S4+S7+S8

S1=S8，S2=S3，S4=S5，S6=S7。

SA+SC=S8+S3+S4+S7=SB+SD

即：SA+SC=SB+SD

 

（三），定理应用：

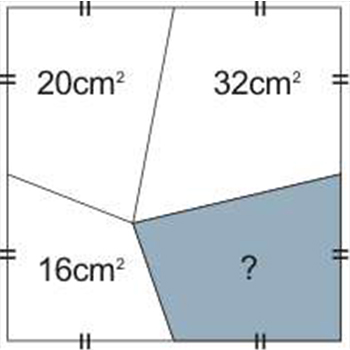
例题：已知正方形部分区域面积，求阴影？

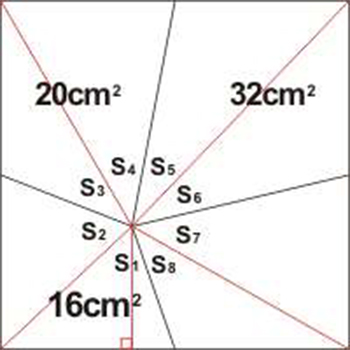
解法一（常规法）：首先将四个四边形分解为八个小三角形并设它们的面积分别为：S1，S2，S3，S4，S5，S6，S7，S8。

在面积为S1的三角形内做垂线可以证明S1=S8。同理：S2=S3，S4=S5，S6=S7。

 

S1+S2+S3+S4+S5+S6=16+20+32

S8+S2+S3+S4+S5+S7=68

S8+S3+S3+S4+S4+S7=68

S7+S8=68-40

S7+S8=28

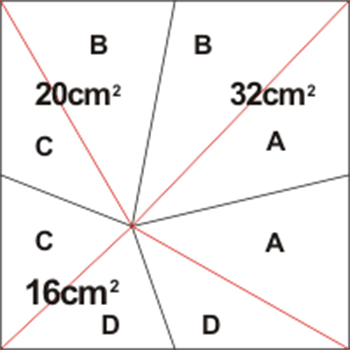
解法二（图形法）：

将四个四边形分解为八个小三角形。因为等底同高的三角形面积相等。故设八个小三角形的面积分别为：A、A，B、B，C、C，D、D。

因为：A+B+D+C=32+16

B+C=20

所以：A+D=32+16-20=28

解法三（定理法）：

 

设阴影四边形面积为X，则

20+X=16+32

X=28

 

二，整数幂个位数的数学命题：

当整数A不等于零时,其5+4n（n为自然数）次幂的个位数等于原整数A的个位数或A本身。
 

作者简介：晏略殊（1973.09---），原名郝立明，曾用名郝栎铭。诗人，爱好数学和哲学。与诗人张智创立了后意象诗派。曾获得《中国诗人》年度诗歌奖、“中国当代诗歌奖”（2017—2018）等奖项。出版诗集《暗河记》《九度九》等。